# 212 Puzzle from the New Scientist
 created by DALL·E
created by DALL·EPuzzle #212 from the New Scientist is:
“Why isn’t the sound working?”, Mum muttered as she hit the mute key on the remote control.
“You’ve probably got the wrong remote, Mum”, Sam said. “Remember, it’s the long, thin one for the television, the wide one for the set-top box and the little one for the speakers. Which one did you mute?”
“I can’t remember”, said Mum, as she got her thinking cap on to try to fix things.
To get sound, all three remotes have to be unmuted. Mum came up with the most efficient system for cycling through the possible combinations of muting and unmuting, and got to work.
What is the maximum number of presses needed if she wanted to be sure of getting the sound back?
Solution
Each remote can be in one of two states {muted or unmuted}. There are three remotes, so in total there are
The desired state is {unmute, unmute, unmute}. We’ll start by finding a system for cycling through the possible combinations of states.
Such a system goes as follows:
- choose a remote and press the mute/unmute key.
- If no sound, press the mute/unmute key again (essentially going back to the initial state). Then repeat step 1, but this time choosing a different remote.
- The worst-case scenario requires 3 presses. We may need to cycle through 1, 2 or all 3 remotes to getting the sound back on.
- If no sound, press the mute/unmute key again (essentially going back to the initial state). Then repeat step 1, but this time choosing a different remote.
- After testing all three remotes in step 1, and provided there is no sound, we start over again but now choosing two remotes together and pressing the mute/unmute keys.
- If no sound, press the mute/unmute key again (reverting to the initial state) and repeat step 2, but this time choosing the other remotes.
- The worst-case scenario this requires 3 presses. That is we can choose, to press remote 1 and remote 2, remote 1 and remote 3, and, remote 2 and remote 3. In total 3 choices.
- If no sound, press the mute/unmute key again (reverting to the initial state) and repeat step 2, but this time choosing the other remotes.
- For the last step, we can press all three remotes simultaneously.
- We count this as 1 press.
So the maximum number of presses is 7: 3 at step 1, 3 at step 2 and 1 at step 3. Note, there is no requirement to follow steps 1 to 3 in this order. Any order works. The trick is to revert the remote(s) to their initial state (which is of course unknown) after each trial.
Code
This R program shows the maximum presses needed to go from any initial state to the unmuted state.
We represent the status of each device using binary values 0 and 1 where muted = 0, and unmuted = 1. So the state {muted, muted, unmuted} is represented with c(0, 0, 1).
library(dplyr)
library(combinat)
library(purrr)
library(ggplot2)
# create a vector to store the status of each device (muted = 0, unmuted = 1)
devices <- c(1, 0, 1) # start from any state
# create a function to check if all devices are unmuted
check_sound <- function(devices) {
sum(devices) == 3
}The function counter() counts the button presses needed to go from any initial state to c(1, 1, 1), i.e. the unmuted state.
# Function to count the button presses for the remotes to achieve state {1, 1, 1} from any initial state.
# The function takes a vector of 3 binary values indicating whether each device is muted (0) or unmuted (1).
counter <- function(initial_state){
if(length(initial_state) != 3){
stop("The function works for only 3 states at the moment.")
}
devices <- initial_state
count <- 0 # initialize a counter for the number of presses
# first check if all unmuted
if (check_sound(devices)) {
out <- count
}
# create look out frame for indices to be changed
g <- expand.grid(1:3, 1:3) %>%
mutate(Var3 = (Var1 == Var2), add = Var1+Var2) %>%
group_by(add, Var3) %>%
slice_sample() %>%
arrange(desc(Var3))
# this is steps 1 and 2 above
for (i in 1:nrow(g)) {
# checks
indices <- g[i,]
devices[c(indices$Var1, indices$Var2)] <- 1 - devices[c(indices$Var1, indices$Var2)] # change 1 or 2 remotes.
if (check_sound(devices)) {
out <- count + 1
} else {
count = count + 1
devices[c(indices$Var1, indices$Var2)] <- 1 - devices[c(indices$Var1, indices$Var2)] # revert to initial state
}
}
# check if changing all fixed the problem - this is step 3 above
devices[c(1, 2, 3)] <- 1 - devices[c(1, 2, 3)]
count <- count + 1 # add 1 count
if (check_sound(devices)) {
out <- count
}
output <- data.frame(initial_state = paste(initial_state, collapse = " "),
count = out)
return(output)
}As an example, if we start from state c(0, 0, 1), and based on the system described above, we need 4 presses1 to get the sound back on.
counter(c(0, 0, 1))$count## [1] 4The plot shows the number of presses needed to get the sound back. Since the code last checks step 3 (pressing all three remotes simultaneously) then if we start from c(0, 0, 0) we are 7 press away from unmuting the TV, which is the worst-case scenario.
In fact, 7 is the maximum number of presses needed, independent of the order steps 1 through 3 are implemented.
# all possible states
states <- list(c(0, 0, 0), c(1, 1, 1),
c(1, 0, 0), c(0, 1, 0), c(0, 0, 1),
c(1, 1, 0), c(1, 0, 1), c(0, 1, 1))
res <- map_dfr(states, counter)
ggplot(res) +
geom_point(aes(x = initial_state, y = count)) +
geom_text(aes(x = initial_state, y = count + 0.5, label = count)) +
labs(x = "Initial State", y = "Number of presses") +
theme_linedraw(12)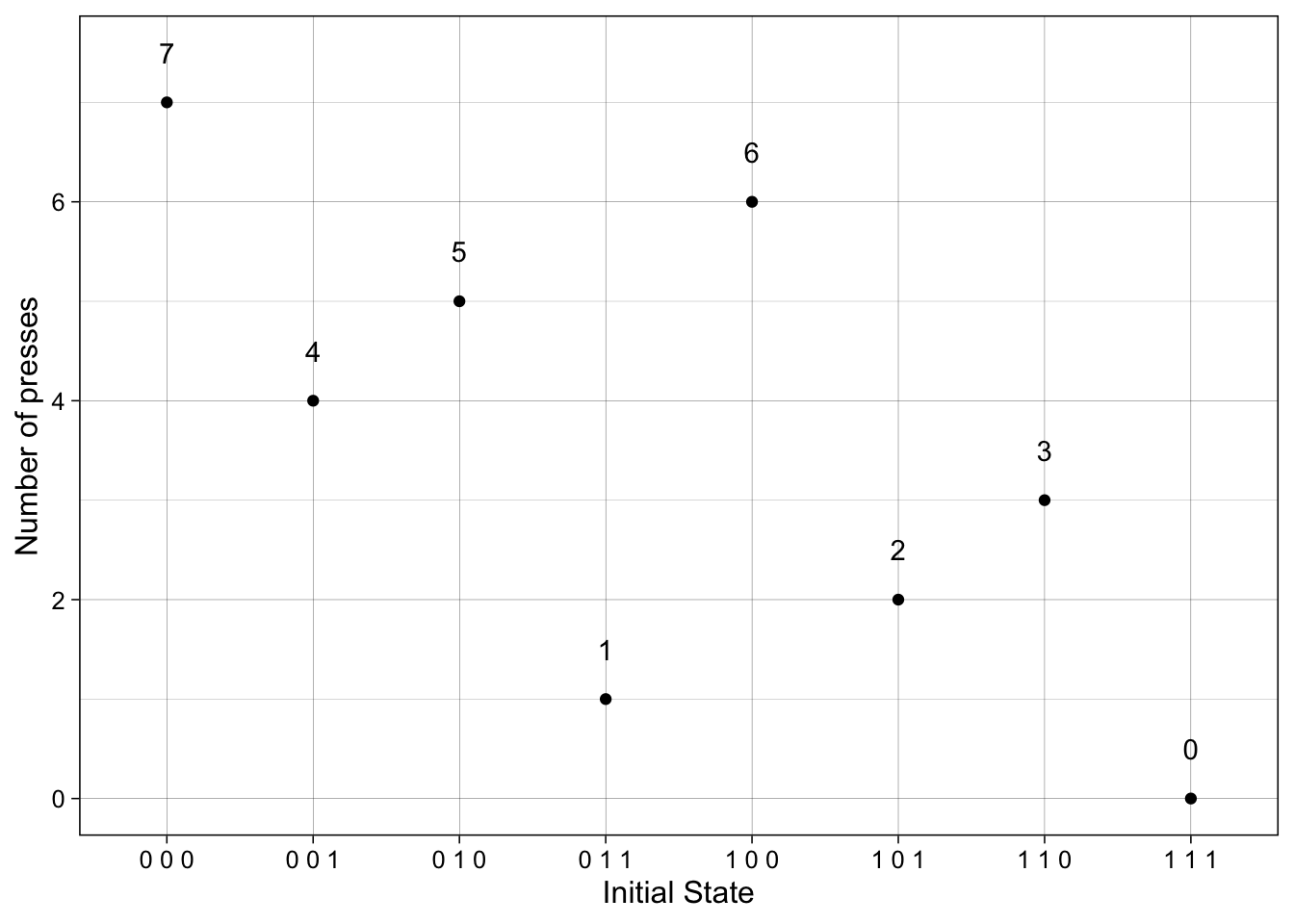
This value depends on how we choose remotes in step 2. The code chooses to change the status of remotes 1 and 2, followed by 1 and 3 and 2 and 3. Hence, when we start from state c(0, 0, 1), we first change one remote at a time (step 1) and then the first and second simultaneously (step 2). This adds up to 4 presses.↩︎