# 204 Puzzle from the New Scientist
created by DALL·EThis week’s puzzle goes as follows:
My son’s book of mathematical magic tricks includes this one:
- Think of a whole number from 1 to 50.
- Add 9 and double the result.
- Multiply by 6 and add 12.
- Subtract 60.
- Divide by 12 and subtract 4.
- Subtract your original number.
- And the answer is (drumroll…) 1!
Unfortunately, when he is reading, my son sometimes repeats a line and sometimes he skips one. That happened with this trick. He did one of the lines twice and then missed the final instruction to subtract this original number. Yet, by an increadible fluke, he still managed to end up on the number 1.
Let’s start by introducing some notation for each step:
- Think of a whole number from 1 to 50 - we call this number \(x\)
- Add 9 and double the result - we call the result of this step, \(q\). That is, \(q=((x + 9)*2)\)
- Multiply by 6 and add 12 - we call this \(r\). That is, \(r = (q*6)+12\)
- Subtract 60 - we call this \(s\). Then, \(s=r-60\)
- Divide by 12 and subtract 4 - we call this \(t\). Then, \(t=\frac{s}{12} - 4\)
- Subtract your original number - we call this \(u\). That is, \(u=t-x\). And, we know, \(u=1\) (from step 7).
The puzzle states that the son “missed the final instruction to subtract this original number.” If he had subtracted the original number (after repeating one of the previous steps) he would have gotten a negative number (or zero). So, we know, after repeating a step that \(t’ \leq 0\), where \(t’\) is the result to step 5, after repeating one of the previous steps.
Now, looking at steps 2 through 5, the only ones that can give us a negative number are steps 4 and 5. Steps 2 and 3 involve the addition and multiplication of positive numbers. They cannot give us a negative result.
We are then left with steps 4 and 5 as potential candidates to have been repeated twice. In fact, whatever the result is after steps 2 and 3 we know that either:
[repeat step 4 twice and add step 5] = 1 (I call this proposition A) or
[step 4 and repeat step 5 twice] = 1 (I call this proposition B).
We can check each of these propositions:
Proposition A is: \(\frac{(r-60)-60}{12} - 4 = 1\). I have simply repeated step 4 twice and then added step 5. Solving for \(r\) gives us \(r = 180\). We can then backtrack, solving for \(q\) from steps 2 and 3 to get \(x =5\). So \(x = 5\) is a potential solution.
Proposition B is: \(\frac{(s/12 - 4)}{12} - 4 = 1\) gives us \(s=768\). From steps 2-4 this implies that \(x=59\), which is outside the range given in step 1. So this is not a valid solution.
Summarizing, the only way to get a result equal to 1 at step 6, after repeating one step twice and then missing the final instruction to subtract the original number, is to choose \(x=5\) at step 1.
Brute force solution
Another way to get the solution is to code steps 2 through 6, repeating each step twice and checking the result for all numbers from 1 to 50. This is what the magic_trick() function does.
# helper functions - each one calculates one of the steps 2-5
f2 <- function(x) (x + 9) * 2 # calculates step 2
f3 <- function(x) (x * 6) + 12 # calculates step 3
f4 <- function(x) x - 60 # calculates step 4
f5 <- function(x) (x / 12) - 4 # calculates step 5
magic_trick <- function(x, rep = 0){
# x: a whole number from 1 to 50
# rep: the step 2-5 to be repeated twice. If rep = 0 or 1. - no repetition
if(rep == 2){
f <- f5(f4(f3(f2(f2(x)))))
} else if(rep == 3){
f <- f5(f4(f3(f3(f2(x)))))
} else if(rep == 4){
f <- f5(f4(f4(f3(f2(x)))))
} else if(rep == 5) {
f <- f5(f5(f4(f3(f2(x)))))
} else {
f <- f5(f4(f3(f2(x)))) - x
}
return(f)
}The code below calculates the final solution to the puzzle for each original number (x_values) and for each step repeated twice or not repeated at all (repeated).
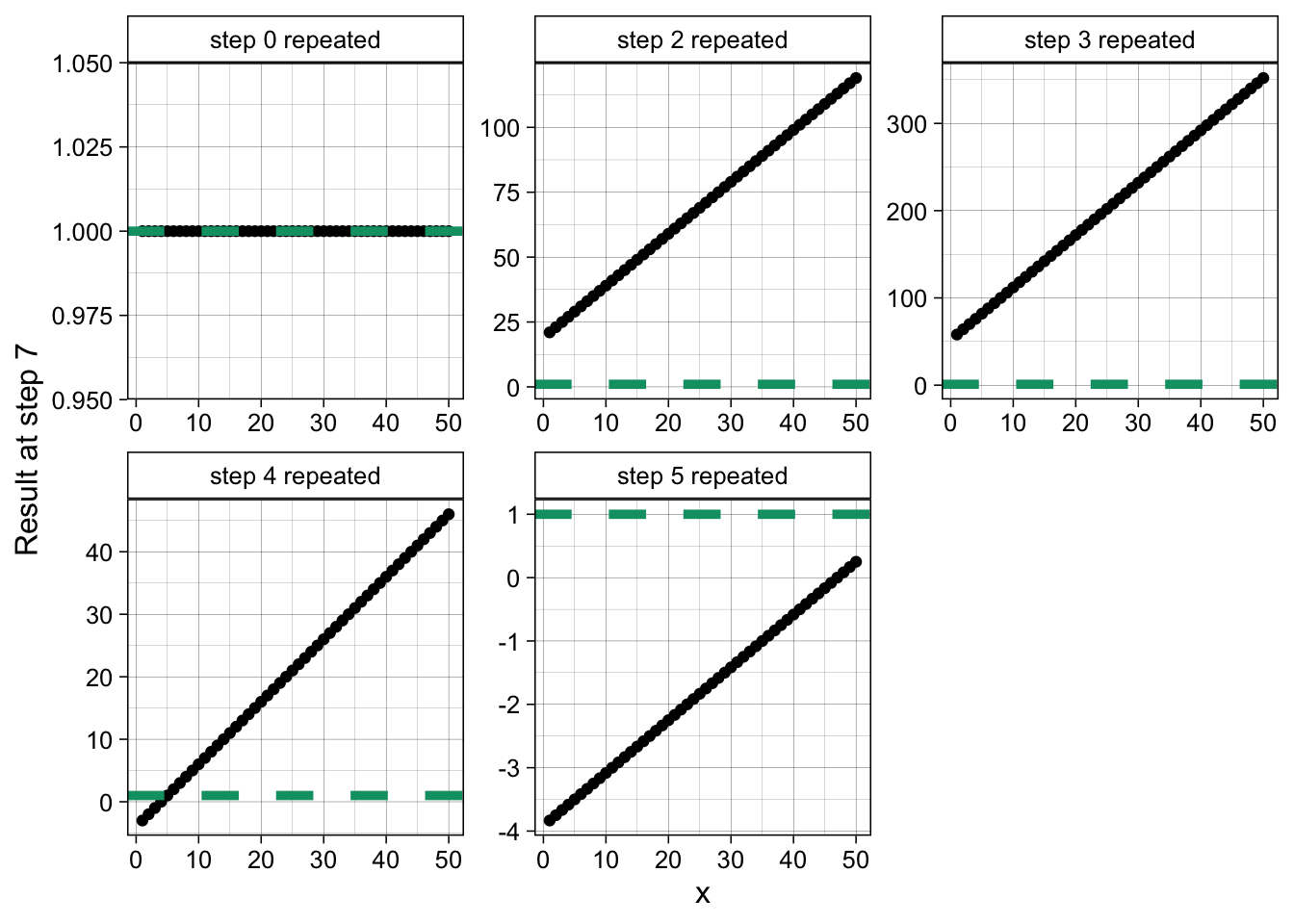
The first (top left) panel corresponds to the solution for the original set-up - no step is repeated. For all \(x\) the result is always one. The second and third panels correspond to repeating steps 2 and 3, respectively. The results confirm our intuition from before - all solutions are positive and well above one. The last panel shows the results when repeating step 5. All of them are negative for the range 1 to 50. Finally, the fourth panel gives the solution to the puzzle. There is only one value of \(x\), namely \(x = 5\), that gives one as the final result.
library(purrr)
library(dplyr)
library(ggplot2)
x_values <- seq(1, 50, by = 1) # step 1: whole number from 1 to 50.
repeated <- c(0, 2, 3, 4, 5) # step to repeat. 0 corresponds to the original puzzle
vals <- expand.grid(x_values, repeated)
res <- map2_dbl(vals$Var1, vals$Var2, magic_trick)
df <- data.frame(x = rep(x_values, 5), repeated = rep(repeated, each = 50), res = res) %>%
mutate(repeated = paste0("step ", repeated, " repeated"))
ggplot(df) +
geom_point(aes(x = x, y = res)) +
facet_wrap(. ~ repeated, scales = "free") +
geom_hline(yintercept = 1, linetype = "dashed", linewidth = 1.7, col = "#009E73") +
labs(y = "Result at step 7") +
theme_linedraw(12) +
theme(strip.background = element_rect(fill = "white")) +
theme(strip.text.x = element_text(color = "black"))
